 |
対空戦・TMD |
|
||||||||
弾道弾の飛翔技術の基礎 |
| 始めに |
| ロケット推進による飛翔段階 (Powered Flight) |
| 大気圏再突入段階 (Re-entry Phase) |
| 再突入弾道の決定 |
| 高熱対策 |
| 弾道の誤差 ← 現在の頁 |
| まとめ |
いよいよ弾道弾で最も肝心な弾道弾の飛翔の誤差、即ち弾道誤差の問題です。
この弾道の誤差はそのまま弾着の誤差に直結することは申し上げるまでもありません。 そして弾道弾が正確に所望の弾道を飛翔するかどうかは、ひとえにその誘導システムの良否にかかってきます。
飛翔第一段階のロケット推進の間に、誘導システムは推進ロケットの燃焼終了時点において弾道弾の速力と方向が所望の速度ベクトルとなるようにコントロールします。 この時に誘導システムが正しく機能しなければ、以後の飛翔において弾道弾の速度ベクトルに次の一つ、あるいはそれ以上の要素の不良を生じることになります。
方位誤差
位置誤差
速力誤差
仰角誤差
当然のことながら、第二段階の自由飛翔においてはこの燃焼終了時点での速度ベクトルの誤差の全てを引き継ぐことになりますが、この段階中に新たな誤差を生じることはありません。
最後の第三段階の大気圏再突入においては、弾道弾は大気の風及び空気密度の変化によって誤差を生じますが、基本的に (GPS等による誘導機能を有しない限り) これらの再突入時の誤差を修正することはできません。
そして 風及び空気密度の変化による弾着誤差は一般的に約1マイル程度以内 であるとされています。
方位誤差は、燃焼終了時の速度ベクトル V* が意図する弾道軌道面上から外れることにより生じる誤差です。 この誤差は、結果として下図に示すように予期弾着点に対して横方向の距離誤差となって現れることになります。
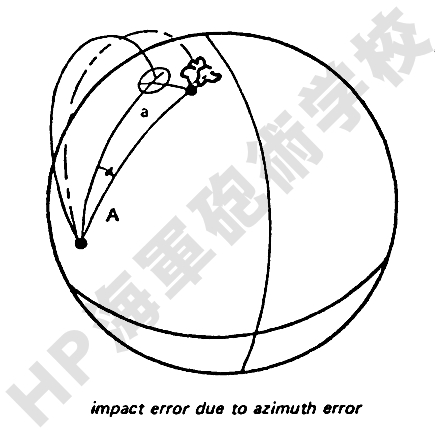
もちろん地球は平面ではありませんから問題はもう少しややこしく、球面三角法によってこの誤差の方程式を求めると次のようになります。
a = A x sin 2θ*
a : 横方向距離誤差 (Cross Range Error) (単位 : マイル)
A : 方位誤差 (単位 : 分)
θ* : 燃焼終了時の本来の弾道方位 (単位:度)
次の図は、この方程式により計算された弾着誤差の一例です。
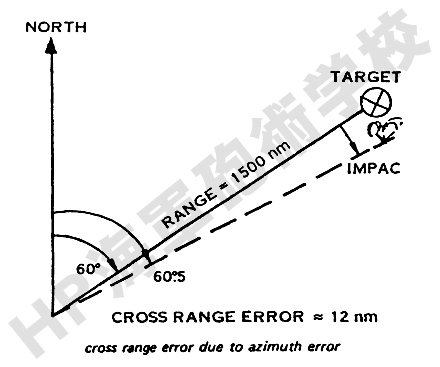
この方程式によりいくつかの方位誤差について作図すると下図のようになります。
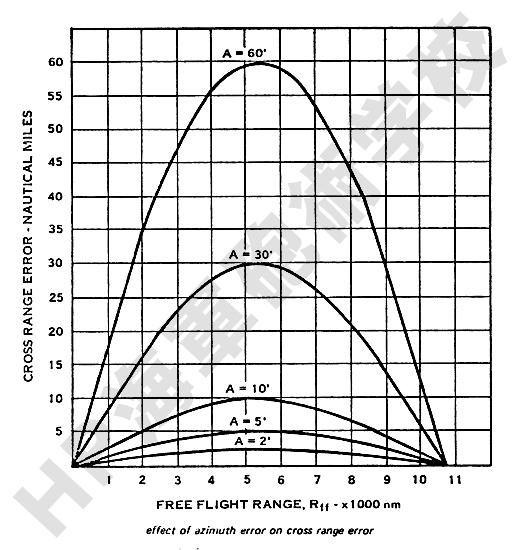
ここで注意していただきたいのは、射程5500マイルのICBMの場合、1度の方位誤差では60マイルの弾着誤差を生じますが、10800マイル (地球周回の約半分) の射程の場合は弾着誤差は 0 (ゼロ) になることです。 これは本来の弾道弾の軌跡と誤差による軌跡は共に地球中心を含む垂直面内にあり、地球の大圏の円を横切ることになるためです。
( これは、例えば1/4や1/8などで切り売りされているスイカなどの皮の表面の形を考えていただければこの理屈がお判りになると思います。)
そしてこの図から、弾着時の誤差を1マイル程度 とするためには、誘導システムは燃焼終了時の速度ベクトルにおいて方位誤差を ±1分の精度 でコントロールする必要があることが判ります。
もし燃焼終了時の速度ベクトルの誤差が位置だけの誤差であるならば、下図に示すように軌道上の全てのポイントを同じ量だけずらしたものと考えることが出来ます。
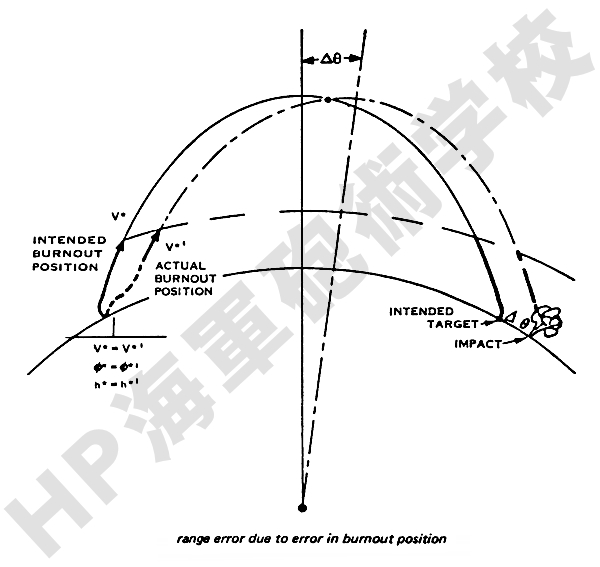
したがって、燃焼終了時の位置がΔθだけずれたとするならば、弾着点も又Δθと同じ量だけずれることになります。 このことは先の (1) の方位誤差の現れ方とは異なりますので注意が必要です。
この燃焼終了時の位置誤差は、次の要素の誤差に起因します。
目標位置データ
打ち上げ位置
誘導
もし目標位置データに誤差があるならば、下図のようにその誤差の距離にほぼ等しい弾着誤差となって現れます。
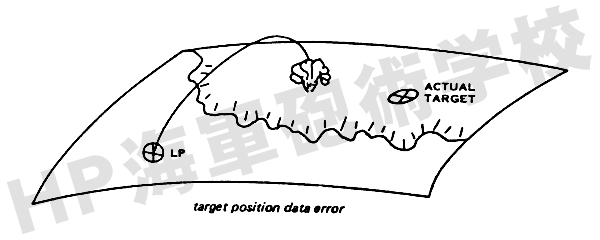
したがって、目標の正確な地理的位置を知ることが必要であることは論を待たないところでしょう。 例えば強固なICBM発射サイトを破壊するには、ほとんど直撃するに足る精密な位置情報が必要になってきます。
またもし移動式発射台を使用する場合、実際の打ち上げ位置が計算位置から1マイルずれているならば、例え弾道が正確に計算されていたとしても、その弾着点は1マイルずれます。
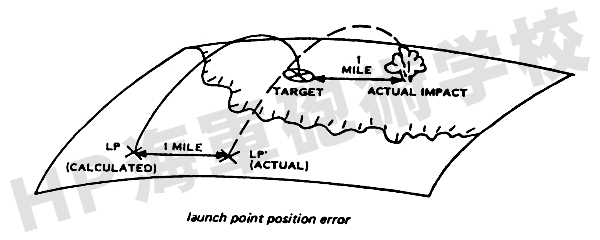
これは、艦船、航空機、あるいは潜水艦から弾道弾を発射するためには、精密な航法機器を装備する必要があることを意味します。
更に、誘導システムが適正な位置で推進ロケットの燃焼を終了させることができなければ、これも正確な弾着を得ることができません。 特に垂直位置の誤差はこの誘導装置の不正確さに起因します。
即ち、例え燃焼終了時に意図した速度 V* 及び仰角 φ* を得たとしも、下図のように燃焼終了位置が高すぎた場合、あるいは低すぎた場合には、弾着位置に誤差を生じることになります。
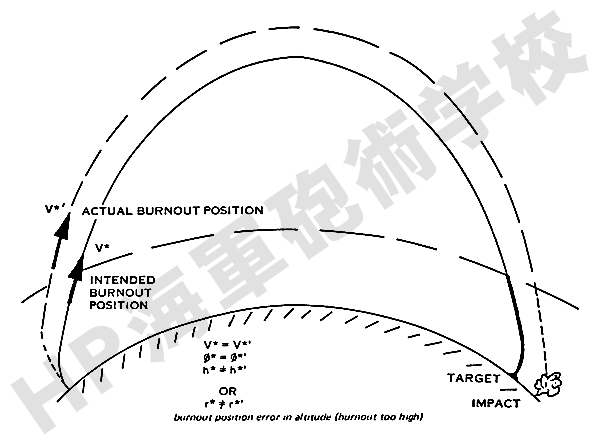
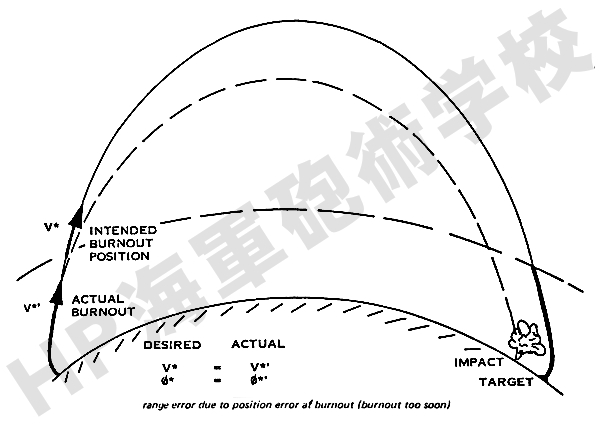
この燃焼終了時の高度誤差は、それによる弾着誤差の決定が他の要素のように1対1的に単純に表されるものではなく、より複雑な方法が必要になります。 例えば、意図した弾道で打ち上げたものの推進ロケットの燃焼終了時が早すぎた場合、本来の燃焼終了位置に達した時点での速度が遅くなることになります。 これによって本来の燃焼終了地点以降の弾道は意図したものより短くなり、これが弾着誤差となります。
したがって、目標位置に弾着させるためには、誘導システムによる燃焼終了位置の極めて正確なコントロールが必要 であることをお判りいただけるでしょう。
ここでいう 「速力」 とは speed、つまり単に早さのことで、方向の要素を含んだ速度 vector のことではありませんのでご注意を。
推進ロケット燃焼終了時における弾道弾の速力の誤差もまた弾着の誤差になることはお判りでしょう。 この速力誤差が生ずると、その後の真空中における楕円軌道が変わり、下図に示すように意図した軌道から長軸を誤差による Δθだけ回転させた新しい楕円軌道になり、その 結果弾着には2Δθの誤差 を生じることになります。
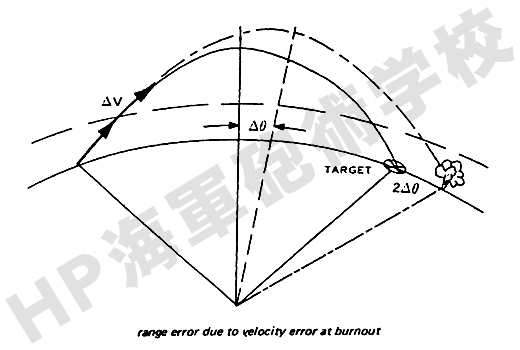
このことは弾道の “高い” “低い” ということと同じ意味になり、これは次の (4) で説明する仰角誤差よりも更に重要な問題となります。
推進ロケット燃焼終了時における弾道の仰角の誤差も弾着時の距離誤差となります。
これも上記の (3) と同じく、意図した軌道から長軸を誤差による Δθ だけ回転させた新しい楕円軌道になり、その 結果弾着には 2Δθ の誤差 を生じることになります。
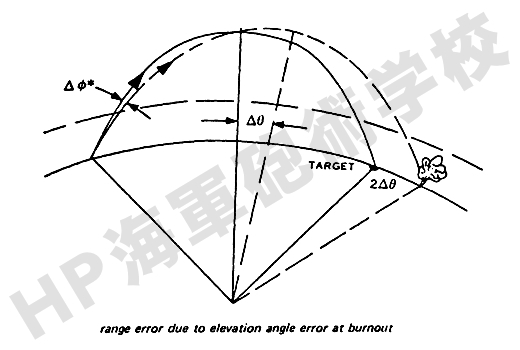
ただし、当初の意図した弾道は所要の射程まで飛翔するに要する最少のエネルギーによるものですから、この仰角誤差は結果的に常に射程の減少となって現れることになります。
最終更新 : 19/May/2017