 |
対空戦・TMD |
|
||||||||
弾道弾の飛翔技術の基礎 |
| 始めに |
| ロケット推進による飛翔段階 (Powered Flight) |
| 大気圏再突入段階 (Re-entry Phase) |
| 再突入弾道の決定 ← 現在の頁 |
| 高熱対策 |
| 弾道の誤差 |
| まとめ |
本項では説明を平易にするため数式などは極力使わない方針ですが、この項だけは少し。 ただし簡単なものですし、読み流していただいても構いません。
といいますのも、既にお話ししたように再突入によって急激な空気抵抗を受けますので、弾道の軌跡がどのようになるかを求めなければ、この段階において弾道弾がどれくらいの距離を飛翔するのかが分かりません。
これは即ち、肝心な弾道弾の発射から弾着までの射程が正確に決められないということになります。 このため再突入体の運動についての方程式を求めることが必要になります。 とは言っても弾道弾の具体的な実際の例を挙げての詳細な説明では頭が痛くなるでしょうから、ここでは一般論としてごく簡単に。
再突入体はその頭部を文字通り頭にして飛翔し、かつピッチ (縦動揺) 及びロール (横動揺) を無視できるような形状に設計します。 これにより、再突入体は弾道に対して小さな迎角を維持するものと仮定することができますから、高速の再突入体に働く外力は重力と空気抵抗がその大部分となります。
ここで、とりあえずは地球は自転していないものと仮定し、そして弾道軌跡の完全な解析には含まれるべき副次的な要素は全て無視して考えることにします。 すると、容積 m、速力 V の再突入体について、弾道軌跡方向の運動方程式は次のように表されます。
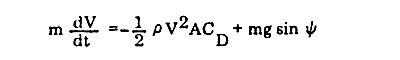
ここで、
ψ : 再突入体の弾軸(縦)方向と水平面とのなす角
ρ : 空気密度
A : 再突入体の有効弾面積
CD : 再突入体の抵抗係数
また、弾道軌跡に対して直角方向の運動方程式は、次のようになります。
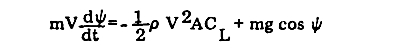
ここで、
CL : 再突入体の揚力係数
再突入の最初の姿勢再変換の段階ではまだ空気密度は小さく、弾体は極めて高速ですので、この段階での飛翔軌跡は直線と見なすことができます。
また、次の減速段階でも再突入体の迎角 (ψ) は小さいので、上の方程式中の右辺の揚力の項はゼロに近くなりますので、この方程式は次のように表すことが可能です。
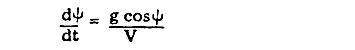
これらのことから、再突入の3段階のうち、初めの2つの間、再突入体の飛翔軌跡は直線と見なしても差し支えないものとされ、実際の検証においてもそれ程大きな誤差は生じないことが明らかとなっています。
なお、この再突入第2段階終期の高度 5万フィート (1.5万m) にける弾体の速度は、まだ 約1万フィート/秒 (約3000m/秒) であることに注意して下さい。 そして、最後の高度5万フィート以下の終末段階においては、弾体の軌跡は再突入の速度にはほとんど関係しません。
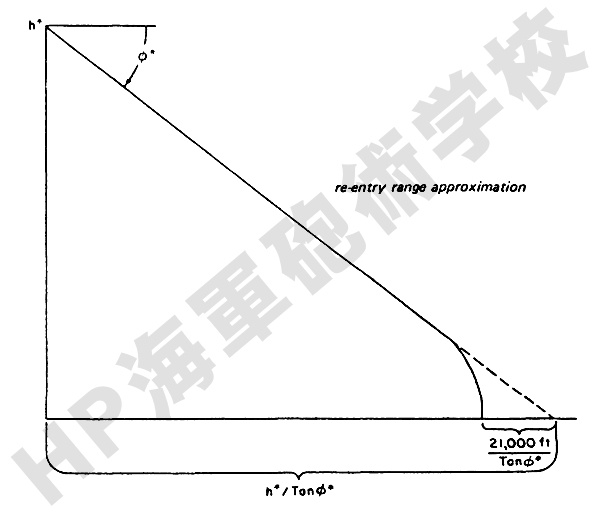
したがって、もしこの終末段階においてもその前の第1及び第2段階と同様に直進である見なした場合との差は、打ち上げ時の燃焼終了点 (Burnout Point) と同高度における再突入角 (φ*) だけに関係することになります。
このことから、通常の弾道弾の速度の範囲においては、 21000フィート/tan φ* (あるいは 3.5マイル/tan φ*) として実際の値とほとんど誤差がないことが知られています。
つまり、再突入段階におい飛翔軌跡の全体が直進であるとすると、その水平距離は次の式となります。
そしてこれに終末段階における弾道軌跡の上記の差を加味すると、
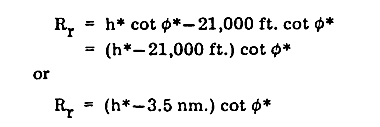
で表されることになります。
次ぎに、再突入段階における弾着までの速度の変化との飛翔秒時についてです。
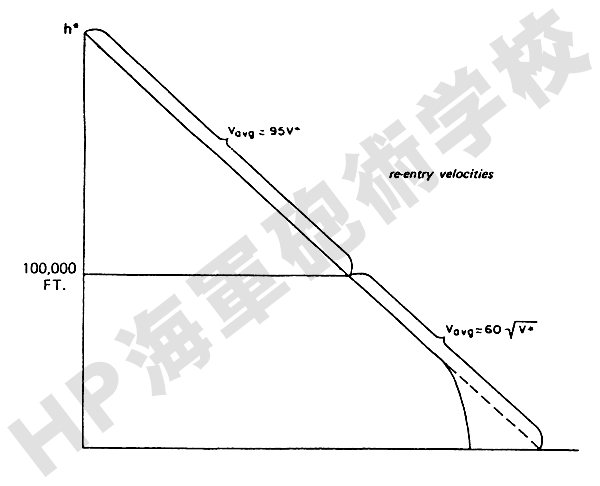
当然ながら空気密度が高くなるにつれて再突入体の速度は空気抵抗のために低下していきますが、再突入第2段階の減速段階途中の高度10万フィート (3万m) まではまだそれ程急激に低下するわけではありません。
再突入からこの 高度10万フィートまでは、平均で 再突入速度 (V*) の 95% であると見なして大差がないことが実証されています。
しかしながら、この高度 10万フィート以下になりますと、再突入体の形状や有効面積などによって大変複雑な関数となります。 とはいっても、一般的に用いられる弾道弾の形状において、再突入速度が 10000 〜 25000 フィート/秒の範囲である場合には、その平均速度は 60 X √V* フィート/秒 としてそれ程大きな誤差とならない ことも知られています。 もちろんより正確な値を求めようとすると、だんだん複雑な計算式になりますが ・・・・
これにより、再突入高度 (h*) から高度 1万フィートまでの水平飛翔距離は
となり、その間に要する飛翔秒時は平均速度 95%を用いて、
となります。 そして、高度 1万フィートから弾着点までの飛翔秒時の計算には、水平飛翔距離として
を使用します。 もちろん前述のようにこれでは大きな誤差となりますが、秒時誤差としてはそれ程大きなものとはならない ことに注意して下さい。
この水平飛翔距離を用いての飛行秒時は
となります。 したがって、再突入から弾着までの飛翔秒時は次の式で得られることになります。
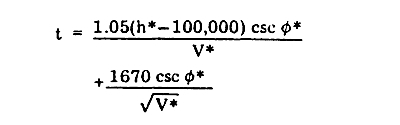
なお、実際の代表的な弾道弾におけるものとして、射程 500マイル (約900km) の SRBM の場合の例と、射程 5500マイル (約10200km) の ICBM の場合の例を示しますと、次のようになります。
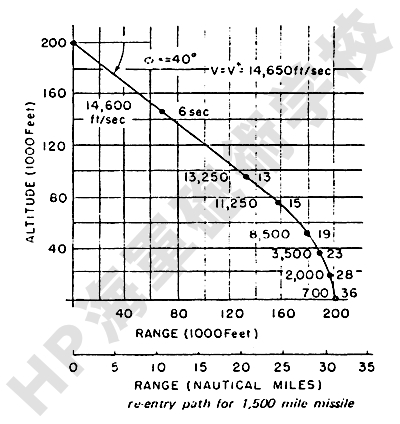
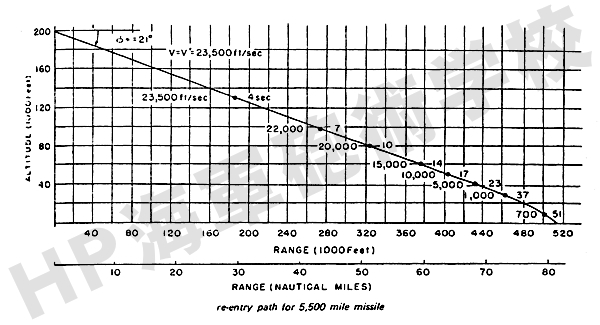
この程度のデータでも、刊行物やネットなどにはまず見当たりませんし、概略を知るためには十分ご参考になるものと思います。
最終更新 : 198/May/2017